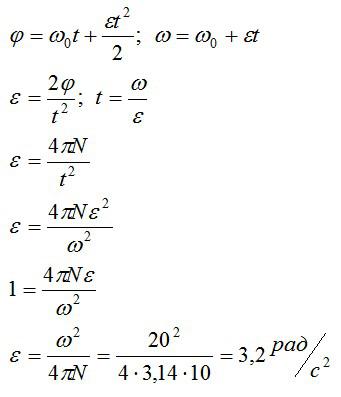Формулы для расчета линейной скорости — простой способ определения скорости передвижения

Движение — одно из основных понятий физики, и его изучение неразрывно связано с понятием скорости. Скорость — это величина, которая характеризует движение тела в определенной системе единиц.

Фактически, скорость — это модуль вектора скорости, который определяется величиной и направлением движения тела. Сама величина скорости измеряется в системе единиц длины и времени, например, в метрах в секунду (м/с).

Одновременно с линейной скоростью можно рассчитать и угловую скорость тела. Угловая скорость характеризует скорость вращения тела вокруг определенной оси и измеряется в радианах в секунду (рад/с).

Для расчета линейной скорости существует несколько формул, их применение зависит от характера движения. В одной из формул участвуют радиус и угловая скорость, в другой — радиус и линейное ускорение.

Особый интерес представляет задача о движении автомобиля по криволинейной траектории. В этом случае возникает парадокс: фактически автомобиль движется прямо, но по кривой линии. Этот парадокс можно объяснить с помощью понятия центростремительного ускорения.

Формулы для расчета линейной скорости

Чтобы определить скорость точки во время вращения или движения по кривой траектории, нужно использовать центростремительное ускорение. Центростремительное ускорение равно произведению модуля линейной скорости на модуль радиуса, по которому движется точка, деленное на время.

Тогда формула для расчета линейной скорости вращения точки по окружности будет иметь вид:

Формула для расчета линейной скорости вращения:

v = r * ω

где v – линейная скорость, r – радиус окружности, ω – угловая скорость вращения.

Аналогично, при движении точки по кривой траектории можно использовать модуль вектора скорости, который равен произведению модуля линейной скорости на модуль радиуса этой криволинейной траектории. В этом случае формула будет выглядеть как:

Формула для расчета линейной скорости на кривой траектории:

v = r * |v|

где v – вектор скорости, r – радиус криволинейной траектории.

Таким образом, для расчета линейной скорости в векторной и не векторной форме, необходимо знать значение радиуса и другие данные о движении точки.

Простой способ определения скорости передвижения

Для определения скорости передвижения объекта в прямолинейном движении можно использовать формулы, которые связывают линейную и угловую скорости.

Данная связь базируется на следующем факте: объект, движущийся по окружности с постоянной скоростью, описывает равномерное вращение вокруг своей оси. Линейная скорость в данном случае характеризуется модулем вектора скорости и всегда равна произведению модуля угловой скорости на радиус окружности, по которой движется объект.

Для того чтобы разобраться в формулах для расчета линейной скорости, рассмотрим пример автомобиля, движущегося по прямой. В данной ситуации автомобиль совершает простое движение, характеризующееся константной линейной скоростью. В то же время, колеса автомобиля связаны с внешним видом движителя ступицы и совершают вращение вокруг оси ступицы с постоянной угловой скоростью.

Для определения линейной скорости автомобиля в данной системе необходимо знать радиус колеса и его угловую скорость. Зная эти данные, можно использовать формулу: скорость = радиус x угловая скорость.

Измеряемый промежуток времени в данном случае является величиной постоянной, поэтому в формуле главное — корректное определение модуля угловой скорости. Угловая скорость равна отношению угла поворота (в радианах) колеса к времени вращения.

Таким образом, задача определения скорости передвижения автомобиля сводится к измерению радиуса колеса и угловой скорости колеса в момент времени. Поскольку радиус и угловая скорость между собой связаны, можно получить фактическую линейную скорость автомобиля на основе этих данных.

Однако необходимо отметить, что в реальных движениях существует парадокс восприятия скорости. Фактическая скорость, которую мы чувствуем во время езды, может отличаться от измеренной. Это связано с векторными характеристиками движения (направление движения, нахождение внешней точки автомобиля на окружности радиуса), а также с определенной задержкой при передаче данных по зрительной системе.

Таким образом, определение линейной скорости в простых задачах движения может осуществляться по формуле, которая связывает линейную и угловую скорости. Для этого необходимо знать радиус и угловую скорость движущегося объекта в момент времени.

Мгновенная и средняя скорости

Для определения скорости передвижения объекта необходимо знать его мгновенную или среднюю скорость. Мгновенная скорость характеризует скорость объекта в определенный момент времени, а средняя скорость определяется средним значением скорости на протяжении заданного временного интервала.

При изучении движения по окружности, такого, как движение планеты вокруг Солнца или движение автомобиля по круговому повороту, мгновенная линейная скорость может быть определена с помощью радиуса окружности и угловой скорости.

Используя центростремительное ускорение, можно определить мгновенную линейную скорость через вектор ускорения и радиус окружности, по которой движется объект. Формула для расчета мгновенной линейной скорости выглядит следующим образом:

Величина линейной скорости = радиус x величина угловой скорости

В случае движения объекта по прямой линии, мгновенную линейную скорость можно определить с помощью формулы:

Мгновенная линейная скорость = модуль вектора скорости

Угловая скорость является величиной, которая задается в радианах за единицу времени. Она характеризует скорость вращения объекта вокруг центра — точки, вокруг которой совершается вращение.

Средняя скорость представляет собой отношение пройденного пути к затраченному времени. В случае движения по окружности, средняя скорость равна длине окружности, деленной на время, которое понадобилось для ее преодоления. Формула для расчета средней скорости выглядит следующим образом:

Средняя линейная скорость = путь / время

Однако, кроме линейной скорости, важны и другие характеристики движения объекта. Например, ускорение является величиной, которая характеризует изменение скорости со временем.

Таким образом, мгновенная и средняя скорость играют важную роль в изучении движения объектов. Зная эти величины, мы можем определить законы движения, решать различные задачи и анализировать перемещение объектов.

Равномерное движение по прямой линии

Определение равномерного движения

Равномерное движение по прямой линии может быть определено путем измерения скорости тела. Для определения этой величины существуют формулы, основанные на характеристиках движения тела. Одна из таких формул — это формула для расчета линейной скорости.

Формула для расчета линейной скорости

Линейная скорость может быть рассчитана с помощью формулы: V = S / t, где V — линейная скорость, S — пройденный путь, t — промежуток времени.

Радиус движения тела также играет большую роль при расчете скорости. В случае, когда движение происходит по окружности радиусом R, то линейная скорость можно определить с помощью формулы: V = R ⋅ ω, где ω — угловая скорость тела.

Примеры равномерного движения

Примером равномерного движения может служить автомобиль, движущийся по прямой дороге с постоянной скоростью. В данном случае, пройденный автомобилем путь S можно вычислить, зная его скорость и время движения.

Другим примером равномерного движения является колесо автомобиля, вращающееся вокруг своей оси. В этом случае радиусом движения будет радиус колеса, а угловая скорость будет определяться скоростью вращения колеса. Линейная скорость точек колеса будет одинакова и равна произведению радиуса колеса на его угловую скорость.

Равномерное движение по прямой линии является одной из простейших задач в физике. С его помощью можно решать различные задачи, связанные с определением скорости и пройденного пути телом. Это позволяет более точно измерять и оценивать скорость движения транспортного средства, а также решать задачи, связанные с его движением.

Линейная скорость и центростремительное ускорение

Решение задачи расчета линейной скорости соединено с задачей определения центростремительного ускорения поскольку эти две величины связаны между собой. Для того, чтобы определить линейную скорость колеса автомобиля в момент времени, можно использовать формулу связи между линейной и угловой скоростями:

Линейная скорость (v)

=

Угловая скорость (ω)

*

Радиус (r)

Тогда в формуле можно определить линейную скорость колеса автомобиля, если известны угловая скорость и радиус колеса. Величина радиуса колеса фактически представляет собой расстояние, которое колесо преодолевает за единицу времени. Сожалению, в реальных задачах мы обычно имеем дело с задачей об определении линейной скорости, а угловая скорость колеса неизвестна. Однако, если в задаче есть информация о времени и расстоянии, пройденных колесом, то угловую скорость можно определить следующим образом:

Угловая скорость (ω)

=

Расстояние (s)

/

Время (t)

Таким образом, решая задачу о движении колеса автомобиля, можно определить его линейную скорость на основе известных величин радиуса колеса, расстояния и времени. Это позволяет получить более точное представление о скорости передвижения транспортного средства в виде линейной величины.

Линейная скорость: формула расчета нахождения

Определение линейной скорости может быть полезно в различных задачах. Например, при изучении траектории автомобиля, вращении тела вокруг оси, расчете равномерного движения и других задачах механики.

Существует несколько формул для расчета линейной скорости в зависимости от конкретной задачи.

Формула для расчета скорости при равномерном движении

Если тело движется с const- линейной скоростью, то простая формула для расчета скорости выглядит следующим образом:

v = s/t

где v — скорость, s — пройденное расстояние, t — время движения.

Формула для расчета скорости при вращении вокруг оси

При вращении тела вокруг оси, его скорость характеризуется двумя компонентами: линейной и угловой скоростью. В данном случае важно определить линейную скорость тела на определенном радиусе.

Формула для расчета линейной скорости при вращении вокруг оси имеет вид:

v = ω * R

где v — линейная скорость, ω — угловая скорость (измеряется в радианах в секунду), R — радиус вращения.

Таким образом, зная угловую скорость и радиус вращения, можно легко определить линейную скорость тела.

Формула для расчета скорости при вращении вокруг центростремительной оси

Если тело вращается вокруг центростремительной оси, его скорость зависит от радиуса вращения и углового ускорения.

Формула для расчета линейной скорости в данном случае выглядит следующим образом:

v = a * R

где v — линейная скорость, a — ускорение (угловое), R — радиус вращения.

Таким образом, можно определить линейную скорость тела на основе данных об угловом ускорении и радиусе вращения.

Задачи с примерами решения

Задача 1

Дана планета с радиусом R = 6371 км. На этой планете тело движется равномерно вокруг центра планеты. Необходимо найти линейную скорость тела.

Решение:

Линейная скорость тела определяется формулой v = rω, где v – линейная скорость, r – радиус окружности, по которой движется тело, а ω – модуль угловой скорости.

Для нашей задачи радиус окружности равен радиусу планеты R, а модуль угловой скорости достаточно определить в радианах в секунду. Поскольку задача указывает на равномерное движение тела, то ω будет постоянной. Модуль угловой скорости равен произведению угловой скорости ω на радиус окружности R: ωR.

Исходя из формулы модуля угловой скорости ω = 2π/T, где T – время нахождения тела в одном полном обороте, можно найти модуль угловой скорости.

Тогда линейная скорость тела можно определить по формуле v = Rω:

Радиус планеты (R)	Время нахождения тела в одном полном обороте (T)	Модуль угловой скорости (ω)	Линейная скорость тела (v)
6371 км	24 часа	2π / (24 * 3600) рад/с	6371 * (2π / (24 * 3600)) км/с

Таким образом, линейная скорость тела в данной задаче будет равна значению, полученному из приведенной формулы.

Задача 2

Автомобиль движется по окружности радиусом 50 м. За какое время он проходит полный оборот на этой окружности?

Решение:

Для решения данной задачи необходимо использовать формулу времени нахождения тела в одном полном обороте T = 2π/ω, где T – время, а ω – модуль угловой скорости.

Радиус окружности в этой задаче равен 50 м, а модуль угловой скорости определить несложно. В данной задаче указано, что автомобиль движется равномерно, следовательно, модуль угловой скорости будет постоянным.

Тогда время движения автомобиля на одном полном обороте можно определить с помощью формулы T = 2π/ω, где ω = v/r – модуль угловой скорости, v – линейная скорость, r – радиус окружности.

Исходя из этого, можно записать

Радиус окружности (r)	Линейная скорость (v)	Модуль угловой скорости (ω)	Время нахождения автомобиля в одном полном обороте (T)
50 м	?	?	2π / v/50

С помощью другой формулы, v = rω, где v – линейная скорость, r – радиус окружности, и ω – модуль угловой скорости, можно выразить линейную скорость через модуль угловой скорости: v = rω.

Используем формулу времени и формулу линейной скорости, чтобы найти время нахождения автомобиля в одном полном обороте:

Радиус окружности (r)	Модуль угловой скорости (ω)	Линейная скорость (v)	Время нахождения автомобиля в одном полном обороте (T)
50 м	?	50 * ω	2π / (50 * ω)

Таким образом, время нахождения автомобиля в одном полном обороте будет равно значению, полученному из приведенной формулы.

Формула линейной скорости вращения

Для определения формулы линейной скорости вращения необходимо знать некоторые величины, такие как радиус траектории движения, угловая скорость и центростремительное ускорение. Они связаны следующей формулой:

Величина линейной скорости = радиус * угловая скорость

Это выражение позволяет найти модуль линейной скорости вращающегося тела в данной точке его траектории движения.

Угловая скорость — это величина, определенная в радианах за единицу времени. Чтобы перейти от угловой скорости к линейной скорости, следует умножить угловую скорость на радиус вращения.

Центростремительное ускорение — это ускорение, с которым точка движется вокруг данной оси. Модуль центростремительного ускорения равен произведению квадрата угловой скорости на радиус траектории движения.

Таким образом, формула линейной скорости вращения позволяет определить скорость тела во время его вращения вокруг заданной точки или оси. Это важное правило, которое упрощает решение задачи нахождения линейной скорости вращения по данным о радиусах и угловых скоростях тела.

Формулы для нахождения линейной скорости

Одной из самых простых формул для определения линейной скорости является формула v = s/t, где v — скорость, s — пройденное расстояние, а t — время, за которое происходит движение. Это основная формула для решения задач по определению линейной скорости в простой системе.

Однако в некоторых задачах требуется определить скорость тела, движущегося по криволинейной траектории. В таких случаях используется формула, основанная на векторной связи между линейной и угловой скоростью тела.

Мгновенная линейная скорость v может быть определена путем умножения мгновенной угловой скорости ω на радиус r, по которому перемещается тело в данный момент времени. Такая связь записывается как v = ω ∙ r.

Например, если тело вращается вокруг некоторой оси с постоянной угловой скоростью, то его линейная скорость будет зависеть от радиуса окружности, по которой оно перемещается. Чем больше радиус, тем больше линейная скорость.

По формуле для определения линейной скорости можно найти модуль скорости автомобиля, который проходит промежуток пути за заданный промежуток времени. Например, если автомобиль проехал 100 км за 2 часа, то для определения модуля скорости применяется следующая формула: v = 100 км / 2 ч = 50 км/ч.

Кроме того, формула для определения линейной скорости может быть использована для расчетов в сферической системе координат. Например, чтобы определить скорость планеты, которая вращается вокруг Солнца по эллиптической орбите, необходимо использовать формулу v = ω ∙ r, где ω — угловая скорость, а r — радиус орбиты.

Примеры решения задачи по определению линейной скорости:

1. Задача: Автомобиль движется со скоростью 80 км/ч. Определите его линейную скорость в м/с.

   Решение: Для этого необходимо преобразовать скорость из км/ч в м/с. Для этого нужно разделить значение скорости на 3,6.

   Ответ: линейная скорость автомобиля составляет 22,22 м/с

2. Задача: Тело движется по окружности радиусом 3 метра со скоростью 2 м/с. Определите его угловую скорость.

   Решение: Для этого нужно использовать связь между линейной и угловой скоростью тела. Угловая скорость будет равна отношению линейной скорости к радиусу окружности.

   Ответ: угловая скорость составляет 0,67 рад/с

Задача на определение линейной скорости нашей планеты

Когда мы наблюдаем за движением автомобиля, мы можем заметить, что колеса вращаются. Вращение колес автомобиля характеризуется угловой скоростью, а передвижение автомобиля — линейной скоростью.

Задача состоит в том, чтобы определить линейную скорость передвижения автомобиля, зная его угловую скорость и радиус колеса.

Формула для расчета линейной скорости в данном случае выглядит следующим образом:

v = ω * r

где:

• v — линейная скорость автомобиля;
• ω — угловая скорость колеса;
• r — радиус колеса.

В нашей задаче у нашей планеты Земля телом, около которого вращаются и движутся другие тела, включая наш автомобиль. Траектория движения автомобиля по совету Сазонова в системе, связанной с поверхностью Земли, является парадоксальной. На самом деле мы движемся вдоль прямой, но по ощущениям, при постоянной скорости, кажется, что движемся по окружности.

Чтобы определить скорость движения нашей планеты, нам необходимо найти связь между угловой скоростью и линейной скоростью. Для этого воспользуемся формулой:

v = ω * r

где:

• v — линейная скорость планеты Земля;
• ω — угловая скорость;
• r — радиус Земли.

Сожалению, у нас нет точных данных о радиусе Земли и угловой скорости, чтобы найти линейную скорость. Однако, зная, что планета Земля совершает равномерное вращение вокруг своей оси за время около 24 часов, мы можем определить среднюю линейную скорость планеты Земля.

Фактически, за время вращения планета Земля проходит около 40000 километров. Используя формулу для расчета окружности с радиусом R, получаем следующую связь между линейной и угловой скоростью:

v = ^2πR/T

где:

• v — средняя линейная скорость планеты Земля;
• R — радиус Земли;
• T — время вращения планеты Земля (24 часа или 86400 секунд).

Таким образом, хотя мы не можем определить мгновенную линейную скорость нашей планеты в данной задаче, мы можем найти среднюю линейную скорость при помощи угловой скорости и радиуса Земли.

Связь между линейной и угловой скоростями

Для понимания связи между линейной и угловой скоростями, рассмотрим пример с вращением колеса автомобиля. Колесо совершает равномерное вращение вокруг своей оси. В этом случае, точка на ободе колеса будет двигаться по окружности с определенной линейной скоростью.

Связь между линейной и угловой скоростями определяется радиусом колеса и угловой скоростью его вращения по формуле:

Линейная скорость = (Радиус колеса) × (Угловая скорость)

Таким образом, если известны радиус колеса и его угловая скорость, можно легко определить линейную скорость точки на его ободе.

Примеры применения данной формулы можно найти во многих задачах. Например, при рассмотрении движения планеты вокруг Солнца. Скорость планеты определяется как линейная скорость точки, находящейся на ее орбите. Угловая скорость планеты в этом случае равна скорости, с которой она вращается вокруг Солнца.

Следует также отметить, что угловая скорость и линейная скорость взаимосвязаны через период времени. Угловая скорость измеряется в радианах на секунду, а линейная скорость – в метрах на секунду.

Однако, сознательно или нет, мы все сталкиваемся с такой задачей по ходу нашей жизни.

К примеру, рассмотрим колесо транспортного средства, которое вращается вокруг своей оси. В этом случае, угловая скорость колеса определяется скоростью его вращения. Используя правило преодоления промежутка, можно найти линейную скорость колеса. Скорость колеса является единицей для измерения скорости самого транспортного средства.

Такое простое и понятное правило помогает нам определить линейную скорость по угловой скорости и радиусу окружности, которую проходит тело. Но, к большому сожалению, всегда не получается найти мгновенную скорость тела в данной системе измерений.

Задача нахождения линейной скорости по угловой скорости может быть решена путем вычисления средней скорости за определенный промежуток времени.

Такое решение задачи позволяет нам найти модуль скорости тела в движении и узнать величину линейной скорости. По формуле можно расчитать скорость тела в виде вектора в данной системе измерений.

Скорость при движении по прямой с ускорением

В предыдущем разделе мы рассмотрели формулу для расчета линейной скорости при прямолинейном равномерном движении. Однако, часто объекты движутся по прямой с ускорением, и возникает вопрос, как определить их скорость в этом случае.

Для того чтобы понять, как определить скорость при движении по прямой с ускорением, рассмотрим пример с автомобилем. Представим ситуацию, когда автомобиль мгновенно ускоряется или замедляется. Мы хотим определить его линейную скорость в каждый момент времени на протяжении всего промежутка времени, в течение которого происходит ускорение или замедление.

Центростремительное ускорение и его связь с линейной скоростью

При движении по окружности тело постоянно меняет направление своей скорости, поэтому оно испытывает центростремительное ускорение. Это ускорение направлено к центру окружности и его величина определяется по формуле:

У_цс = v²/r

где v — линейная скорость тела, r — радиус окружности.

Теперь рассмотрим случай движения по прямой. Для того чтобы связать центростремительное ускорение с линейной скоростью при прямолинейном движении, представим, что тело движется по окружности с бесконечно большим радиусом. В этом случае центростремительное ускорение практически равно нулю, и скорость тела находится в одной и той же точке окружности на протяжении всего движения.

Таким образом, при движении по прямой тело фактически движется по окружности с бесконечно большим радиусом, и линейная скорость тела в любой момент времени равна модулю мгновенной скорости при вращении тела по такой окружности с радиусом r.

Нахождение мгновенной скорости при вращении тела

Теперь рассмотрим, как можно определить мгновенную скорость при вращении тела по окружности с радиусом r. Для этого введем понятие угловой скорости ω, которая измеряется в радианах в единицу времени.

Угловая скорость определяется по формуле:

ω = Δθ/Δt

где Δθ — изменение угла вращения, Δt — промежуток времени.

Мгновенная скорость при вращении тела определяется как предел отношения изменения угла к промежутку времени, стремящемуся к нулю:

v = lim_Δt→0(Δθ/Δt)

Мгновенная скорость при вращении тела будет равна угловой скорости умноженной на радиус окружности:

v = ω * r

Теперь мы можем использовать эту формулу для определения линейной скорости при движении по прямой с ускорением, поскольку она фактически представляет собой мгновенную скорость при вращении объекта с бесконечно большим радиусом.

Примеры задач

Рассмотрим несколько примеров задач, чтобы проиллюстрировать применение этого правила в различных ситуациях.

Пример 1: Автомобиль движется по прямой с постоянным ускорением 5 м/с². Найдите его линейную скорость через 10 секунд с начала движения.

Решение: Для решения этой задачи мы можем использовать формулу v = ω * r. Так как угловая скорость и радиус равны нулю (так как движение происходит по прямой), линейная скорость будет также равна нулю.

Пример 2: Колесо радиусом 0,5 м вращается со скоростью в 40 рад/с. Найдите линейную скорость точек колеса на его периферии.

Решение: Мы можем использовать формулу v = ω * r для нахождения линейной скорости точек колеса. Подставив значения скорости (40 рад/с) и радиуса (0,5 м) в формулу, получаем:

v = 40 рад/с * 0,5 м = 20 м/с

Таким образом, линейная скорость точек колеса равна 20 м/с.

В этом разделе мы рассмотрели, как определить линейную скорость при движении по прямой с ускорением. С помощью связи между центростремительным ускорением и линейной скоростью при вращении объекта, мы можем вывести формулу v = ω * r для определения линейной скорости. Это правило может быть использовано для решения задач, связанных с движением по прямой с ускорением и вращением тел.

Вращение тел

В отличие от линейной скорости, которая определяется как перемещение тела по прямой линии за определенное время, скорость вращения тела характеризуется угловой скоростью. Угловая скорость определяется как отношение угла поворота к пройденному пути. Также можно выразить угловую скорость через линейную скорость и радиус траектории точки на теле по формуле:

ω = v / r

где ω — угловая скорость, v — линейная скорость, r — радиус траектории точки на теле.

Для расчета линейной скорости тела, движущегося по траектории в виде окружности, можно использовать такую формулу:

v = ω * r

Таким образом, скорость точек тела, перемещающегося по окружности, пропорциональна их расстоянию от центра вращения.

Вращение тела также характеризуется угловым ускорением, которое определяется как изменение угловой скорости за единицу времени. Угловое ускорение обычно обозначается буквой α.

Для тел, вращающихся с постоянным угловым ускорением, справедлива формула:

α = Δω / Δt

где α — угловое ускорение, Δω — изменение угловой скорости, Δt — изменение времени.

Мгновенная линейная скорость точки тела находится при помощи производной от угловой скорости по времени:

v = r * dω / dt

Таким образом, мгновенная линейная скорость точки тела зависит от радиуса траектории и угловой скорости.

Кроме того, центростремительное ускорение — это ускорение, которое всегда направлено к центру вращения и его величина равна произведению квадрата угловой скорости на радиус траектории точки:

a = ω² * r

Центростремительное ускорение для тела, движущегося по окружности с постоянной скоростью, всегда направлено к центру окружности и равно скорости деленной на радиус окружности.

Видео:

Урок 88 (осн). Линейная скорость точки на вращающемся теле

Урок 88 (осн). Линейная скорость точки на вращающемся теле by Павел ВИКТОР 65,971 views 5 years ago 38 minutes