- Цикл работы и особенности рабочего тела идеального газа в тепловом двигателе
- Решебник Трофимова Т.И. 1999 — Задача 2.66
- Условие задачи
- Решение задачи
- Определение начальной и конечной температуры:
- Решебник Трофимова Т.И. 1999 — Задача 2.71
- Решение задачи 2.70 из решебника Трофимова Т.И. 1999
- Дано:
- Решение задачи:
- Решебник Трофимова Т.И. 1999 — Задача 2. 72
- Основы термодинамики
- 1. Цикл работы идеального газа
- 2. Изотермический процесс
- 3. Адиабатический процесс
- Решебник Трофимова Т.И. 1999 — Задача 2. 73
- UptoLike
- Решебник Трофимова Т.И. 1999 — Задача 2. 69
- Решебник Трофимова Т.И. 1999 — Задача 2. 65
- Видео:
- Термодинамика | КПД, Цикл Карно и тепловой двигатель | ТЕХНОСКУЛ
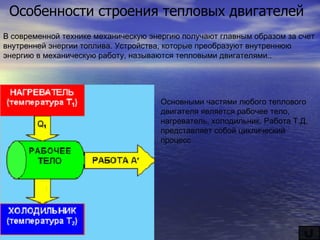
Цикл работы и особенности рабочего тела идеального газа в тепловом двигателе
Рабочее тело в тепловом двигателе — это вещество, которое работает внутри двигателя, занимающий определенный объем и создает работу, получая теплоту от внешнего источника. В идеальном газе равными массами занимающих одинаковые объемы при одинаковой температуре. В реальных процессах, конечно, не все эти условия выполняются.
Если предположить, что газ воздействует на поршень и этот поршень ограничивает рабочее пространство, то можно получить некоторую диаграмму, на которой изобразить процесс преобразования газа. На этой диаграмме можно отобразить процессы внутрициклическими кривыми, например, изохорным (процесс, при котором объем газа не изменяется), изобарным (при котором давление газа не изменяется), изотермическим (процесс, при котором температура газа не изменяется) и т.и. При этом, объем газа изменяется в процессах, но верно, что сумма изменений объема газа в процессах 1->2 (изобарного) и 3->4 (изобарного) равна изменению объема газа во всем цикле.
В идеальном моноатомном газе, например, азоте, 70-71% внутренней пространства газа занимает азот N2, а 29-30% образованы кислородом, аргоном и другими газами. Приближенно можно считать, что воздух состоит только из азота и который изменяется внутри теплового двигателя. Если моли воздуха в газе 1 и газ 2 равно, температура газа в 1 процессе будет 65 градусов по Цельсию, а в газе 2 температура будет равна 66 градусам по Цельсию (двухатомный азот). Значит в исследуемом цикле газ нагревается и увеличивает делить температур внутри цикла.
Решебник Трофимова Т.И. 1999 — Задача 2.66
В данной задаче рассматривается тепловой двигатель, работающий с идеальным газом. Задача состоит в определении характеристик цикла работы двигателя на основе данных, предоставленных в учебнике Трофимова Т.И. 1999.
Условие задачи
В результате адиабатическому сжатию 1 моль азота в тепловом двигателе давление увеличилось в два раза, а объем уменьшился в 9 раз. Затем заслонка была закрыта и газ участок участке изобарному нагреваются до начальной температуры при постоянном давлении. После этого иностранный газ разве отправилась к работе expulsion расширяются до ricompression начального объема. Определить работу двигателя, выполняемая на данном процессе. Нарисуйте соответствующую карту.
Решение задачи
Определим начальное и конечное состояния газа в соответствии с условиями задачи:
- Для адиабатического сжатия: Pнач = P, Vнач = V и Tнач = T.
- При изобарном нагревании: Pкон = 2P, Vкон = V/9 и Tкон = T.
- Для экспанзии: Pнач = 2P, Vкон = V и Tкон = T.
Используя уравнение состояния идеального газа PV = nRT, где P — давление, V — объем, T — температура, n — количество вещества газа и R — универсальная газовая постоянная, можно найти начальные и конечные значения температуры для каждого процесса.
Определение начальной и конечной температуры:
Для адиабатического процесса:
PVγнач = const
T1/P1γ-1 = Tнач/Pγ-1
Так как Pнач = P, Vнач = V и Tнач = T, можно записать:
T/Pγ-1 = Tнач/Pγ-1
Отсюда следует:
Tнач = T/Pγ-1
Для изобарного процесса:
Vкон = V/9 и Pкон = 2P
Используя уравнение идеального газа, можно записать:
PV = nRT
Tкон = PV/(nR) = 2P(V/9)/(nR) = 2T/n = 2T
Для процесса сжатия:
V = V/9 и P = 2P
Используя уравнение идеального газа, можно записать:
Tкон = PV/(nR) = 2P(V/9)/(nR) = T/n = T
Решебник Трофимова Т.И. 1999 — Задача 2.71
В данной задаче рассматривается тепловой двигатель, работающий с рабочим телом в виде двухатомного газа, такого как азот или кислород. Задача состоит в исследовании цикла работы этого двигателя и определении различных параметров.
В начале задачи указаны следующие данные:
- Рода газа — двухатомный (азот или кислород)
- Температура пруда — 65 градусов
- Изначальное давление в пруду — 70 атм
В процессе исполнения цикла работы использованы следующие процессы:
- Изотермический процесс, в котором газ нагревается от начальной температуры пруда до конечной температуры.
- Изобарный процесс, в котором газ расширяется при постоянном давлении.
- Адиабатический процесс, в котором газ нагревается без передачи тепла.
При анализе цикла работы теплового двигателя учитываются основные принципы термодинамики:
- Внутренняя энергия газа может изменяться только в результате внешней работы и теплового воздействия.
- Диаграмма, находящаяся в задаче, показывает зависимость давления от объема газа.
Решение задачи начинается с анализа процессов, которые происходят в рабочем теле:
- При запуске цикла начинается изотермический процесс: газ нагревается от температуры пруда до конечной температуры.
- Затем следует изобарный процесс, в котором газ расширяется при постоянном давлении.
- Далее идет адиабатический процесс, в котором газ нагревается без передачи тепла.
- Наконец, происходит обратный изохорный процесс, при котором газ снова нагревается до начальной температуры пруда.
В конце решения задачи необходимо найти значения объема и давления для каждого из процессов, а также внешнюю работу, совершенную в ходе цикла.
Используя значения температуры и давления, указанные в задаче, можно рассчитать все неизвестные параметры. Задача предоставляет достаточно информации для определения всех значений объемов и давлений в различных тепловых процессах.
Решение задачи 2.70 из решебника Трофимова Т.И. 1999
Дано:
В задаче предоставлено:
- Газ — азот (двухатомный газ);
- Начальное значение массы газа — 66 моль;
- В процессе газ нагревается, и его температура увеличивается до конечной точки процесса;
- Процесс идет на участке диаграммы, соответствующем изобарному процессу;
- На данном участке газ претерпевает увеличение объема согласно изотермическому процессу;
- При учете всех процессов работа заданного цикла равна 2.2 МДж;
- Давление газа в начале процесса равно 71 атм;
- Указана конечная температура газа после процесса.
Решение задачи:
Для решения задачи необходимо применить уравнение состояния идеального газа (газовое уравнение), а также учесть особенности каждого из процессов в идеальном тепловом цикле.
По данным задачи, первым процессом является изохорический процесс, в котором газ нагревается при постоянном объеме. Это означает, что работа в этом процессе равна нулю.
Затем следует изобарный процесс, в котором газ расширяется при постоянном давлении, соответствующем начальному значению — 71 атм. Работу, совершаемую газом в этом процессе, можно найти, используя формулу:
работа = давление * (конечный объем — начальный объем)
После этого идет изохорический процесс, в котором работа снова равна нулю, так как объем газа остается постоянным.
Завершающим процессом цикла является изотермический процесс, в котором газ сжимается или расширяется при постоянной температуре. В этом процессе работа снова может быть найдена с использованием газового уравнения, а именно:
работа = const * (конечная температура — начальная температура) * 2.303 * T / M * log(V1/V2)
Где:
- const — постоянная;
- T — температура газа в Кельвинах;
- M — молярная масса газа;
- V1 и V2 — начальный и конечный объемы газа соответственно.
Таким образом, для решения задачи необходимо каждую из работ в процессах цикла суммировать и получить итоговую работу газа.
Дополнительно следует учесть, что азот является двухатомным газом, у которого коэффициент сжимаемости невелик. Поэтому его можно считать идеальным газом.
В данной задаче важно правильно определить каждый процесс цикла и учесть все входящие в него параметры для получения верного результата.
Итак, решив данную задачу, можно найти величину работы, совершаемой идеальным газом в заданном тепловом двигателе.
Решебник Трофимова Т.И. 1999 — Задача 2. 72
Имеется рабочее тело — 2 моль азота, находящегося в начальном состоянии при температуре Т1 = 65 °C и объеме V1 = 69 литров. Газ нагревается от изотермы при постоянной температуре на участке 65°C до температуры Т2. Следующий участок равен адиабатическому процессу расширения газа от объема V2 = 69 литров до объема V3 = 70 литров при температуре Т3°C. На последнем участке газ увеличил свою температуру на ΔТ по сравнению с Т3 и вернулся к начальному объему V1 согласно процессу расширения при постоянной энтропии. Определить ΔТ и температуры Т2, Т3 по цифрам 2.2, 68 и 73.
В решении задачи необходимо учесть основные принципы термических процессов и применить соответствующие формулы и уравнения. Также важно знать особенности работы идеального газа в тепловом двигателе и уметь применять их в задачах.
Основы термодинамики
Термодинамика изучает превращения и передвижения энергии. Она изучает, как работают тепловые двигатели, такие как двигатели внутреннего сгорания, паровые турбины и тепловые насосы. Рассмотрим основы термодинамики и их применение к работе тепловых двигателей, в частности, к рабочему телу идеального газа в тепловом двигателе.
1. Цикл работы идеального газа
Рабочее тело идеального газа в тепловом двигателе проходит процесс циклической работы, который состоит из нескольких последовательных процессов. Одним из таких циклов является цикл Карно. Он состоит из четырех процессов: изотермического расширения, адиабатического расширения, изотермического сжатия и адиабатического сжатия. В каждом из этих процессов происходят определенные изменения в рабочем теле.
2. Изотермический процесс
В идеальном газе изотермический процесс означает, что температура газа остается постоянной в течение всего процесса. При подаче теплового потока на газ, он расширяется и сжимается медленно, что позволяет рабочему телу передавать положительную работу во внешнюю среду, сохраняя при этом постоянную температуру.
3. Адиабатический процесс
В адиабатическом процессе не происходит теплообмена между рабочим телом и окружающей средой. Подводимый тепловой поток используется только для совершения работы механическими силами. В этом процессе газ сжимается или расширяется быстро, что приводит к изменению его температуры, без обмена теплом с окружающей средой.
Термодинамический цикл работы идеального газа в тепловом двигателе сначала нагревается в изотермическом процессе, затем расширяется в адиабатическом процессе, после чего сжимается в изотермическом процессе и, наконец, снова сжимается в адиабатическом процессе. Такой цикл обеспечивает переход газа через различные температуры и объемы и позволяет получить полезную работу из теплового энергетического источника.
Решебник Трофимова Т.И. 1999 — Задача 2. 73
В данной задаче газом является двухатомный азот и кислород. В начальном состоянии газ находится в пруда с объемом 65 м3 и температурой 66 K. Газ нагревается током, температура газа увеличивается до 68 K. Затем газ расширяется до объема 72 м3, при этом температура остается const и равна 68 K. После этого газ охлаждается изотермически до 66 K, затем происходит адиабатическое сжатие газа, его объем сжимается до начального объема.
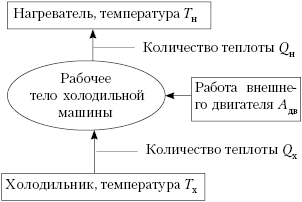
Основы термодинамики учатываются при решении данной задачи. Внутренняя энергия и энтропия газа изменяются на разных участках цикла. Термический двигатель, работающий по такому циклу, создает рабочее тело газом, который нагревается и охлаждается. При этом энергия, которую газ отдаёт при охлаждении, используется для совершения работы внешним телом, например, током, который нагревает газ. В данной задаче требуется определить работу, совешаемую газом внешним телом, и сравнить ее с работой газа над окружающими телами.
UptoLike
Цикл работы теплового двигателя на рабочем теле идеального газа заключается в четырех основных процессах: изотермическом расширении, адиабатическом сжатии, изотермическом сжатии и адиабатическом расширении. Данный цикл основывается на основных принципах термодинамики.
Уравнение состояния для идеального газа можно записать в следующей форме:
pV = nRT
где p — давление газа, V — объем газа, n — количество вещества (в моль), R — универсальная газовая постоянная и T — температура газа.
Перед началом цикла работы, система запускается в тепловом контакте с внешним источником тепла при постоянной температуре. Температура на данном участке процесса равна начальной температуре рабочего тела.
На диаграмме энтропии-объема (т-с) процесс идет от точки 1 до точки 2. При изотермическом расширении газ медленно и равномерно расширяется под воздействием внешнего тепла. Температура на этом участке процесса остается постоянной и равной начальной температуре теплового двигателя.
Давление газа уменьшается, а его объем увеличивается. В результате производится работа контура, а также заваляется некоторая энергия. В объеме n моль газа азота теплота, затрачиваемая на это известна и равна:
Q = nRTln где T — температура газа на участке расширения, V2 — конечный объем газа, V1 — начальный объем газа. После изотермического расширения газ проходит адиабатическое сжатие, то есть без участия внешнего источника тепла. На диаграмме процесс изображается ветвью, ближайшей к линии падения температуры. По первому закону термодинамики применимому только к адиабатическому процессу можно получить что: T1 * V1 ^ (g-1)= T2 * V2 ^ (g-1) где g — показатель адиабаты двухатомного газа, принимаемый равным 1,4 для воздуха и равным 1,67 для азота и кислорода. На следующем участке процесса тепловое состояние газа возвращается к изотермическому. Тепловая энергия газа передается через вентиль до получателя, который нагревается и в свою очередь передает энергию окружающей среде. Если сравнить энергии, получающей газ системы и отдаваемой газом системы: Qполучатель= Cполучателя(T4-T1) Теплота получателя равна разности теплоемкостей контура внешней среды (Cполучателя) и разности начальной и конечной температур системы и получателя (T4 — T1). Таким образом, энергия, которая используется для совершения работы контура, равна разности энергии, полученной газом системы, и энергии, отданной газом системы. Значит, работа контура равна разности внутренней энергии газа на начале и конце цикла и энергии, переданной окружающей среде через получатель. Работа контура равна: Ar = nRT1ln(V2/V1)-C(T4-T1) где T — температура газа на участке идеального расширения и сжатия, V2 — объем газа на участке 2, V1 — объем газа на участке 1, C — теплоемкость внешней среды, T4 — температура окружающей среды, T1 — начальная температура газа. В идеальном случае (без учета энтропии) внутренняя энергия газа изменяется только на изотермическом и адиабатическом участках процесса. Суммарная работа контура, совершаемая газом, обозванная в полной совершенность тепловым кругооборотом, равносильна работе, выполняемой процессами изотермического расширения и сжатия: Ар_сов = nRT1ln(V2/V1) КПД теплового двигателя можно вычислить по формуле: η = (Aр/nQп)х100% где Aр — работа, совершаемая газом системы, Qп — потребляемая калиевая теплота на один тепловой цикл. Таким образом, процесс работы идеального газа в тепловом двигателе, используя азот вместо воздуха, обладает определенными характеристиками и основами термодинамики, которые могут быть использованы для решения задач в данной области. По условию задачи в начальный момент идеальный газ находится в состоянии 1, где его объем равен 68 моль, а температура равна 66 градусам Цельсия. Далее процесс идет в двух этапах: изотермическом (состояния 1-2) и адиабатическом (состояния 2-1). На изотермическом процессе температура газа не изменяется и остается равной 66 градусам Цельсия. Работу учитываем, поэтому можем использовать формулу Q = W = pVln(V2/V1). Данная формула позволяет найти работу процесса для вида изотермического расширения. Учитываем, что здесь энергия изменяется только внутри системы, представленной тепловым двигателем, а значит работа совершается к телу теплового двигателя. Также учитываем, что объем изначально составлял 68 моль, а в конце процесса увеличился до 70 моль (согласно условию задачи). Далее рассматриваем адиабатический процесс. В данном процессе тепловая энергия не обходится никакими процессами, то есть Q = 0. Таким образом, используем формулу для работы процесса, но без учета теплоты. Важно учесть, что температура газа изменяется в этом процессе, и мы можем использовать формулу W = Cv(T2 — T1), где Сv — удельная теплоемкость азота при постоянном объеме (в нашем случае это двухатомный газ азот). Температура меняется, поэтому температуры T1 и T2 будут разные и равными 66 и 73 градусам Цельсия соответственно. Теперь, зная эти данные, можно рассчитать работу каждого из процессов по формуле. Изолируем значения и рассчитаем суммарную работу. В нашей задаче процесс обратим, и значит суммарная работа процесса будет равна нулю. Таким образом, решение данной задачи из Решебника Трофимова Т.И. 1999 — Задача 2. 69: В итоге, решение задачи состоит в нахождении значений энергии и работы каждого из процессов, а также суммарной работы процесса. В задаче указано, что газ находится в начальном состоянии с температурой Т1 и давлением Р1, занимающий некоторый объем V1. Затем газу сообщается тепловой поток установившейся током среды. Изначально среда имеет постоянную температуру, которая устанавливается давлением газа в середине цикла. В задаче также указано, что теплообмен с окружающей средой отсутствует, что означает, что газ находится в тепловой изоляции и не разделяет свою энергию с внешним окружением. Цикл работы состоит из следующих процессов: Изохорное нагревание газа от начального состояния до некоторой температуры Т2. Изохорное охлаждение газа с температуры Т2 до некоторой температуры Т3. Изобарное расширение газа при давлении Р3. Изобарное сжатие газа при давлении Р2. Дано, что в задаче основывается на различных физических законах и свойствах идеального газа, согласно которым предполагается, что газ обладает некоторыми основными характеристиками: Внутренняя энергия газа зависит только от его температуры и может быть изменена только за счет теплового входа. Энтропия газа также зависит только от его температуры и изменяется только за счет теплового входа. В данной задаче рассматривается идеальный газ, который подчиняется закону Гей-Люссака (обычно называемым «обратным законом Амонтилладо»): отношение давления и объема газа при постоянной массе и температуре является пропорциональным. В зависимости от условий задачи для идеального газа могут быть использованы различные уравнения состояния, например, уравнение Менделеева-Клапейрона-Матиоса или уравнение Ван-дер-Ваальса. В данной задаче необходимо определить, верны ли некоторые утверждения о процессах и свойствах газа, учитывая законы и основы термодинамики. Термодинамика | КПД, Цикл Карно и тепловой двигатель | ТЕХНОСКУЛ by ЕГЭ ФИЗИКА I НИКОЛАЙ НЬЮТОН 12,211 views 3 years ago 12 minutes, 32 secondsРешебник Трофимова Т.И. 1999 — Задача 2. 69
Решебник Трофимова Т.И. 1999 — Задача 2. 65
Видео:
Термодинамика | КПД, Цикл Карно и тепловой двигатель | ТЕХНОСКУЛ